+ 항공대학교 이인복 교수님의 알고리즘 해석 및 설계 과목 내용를 정리한 글입니다.
힙 정렬 (Heapsort)
버블 정렬과 비슷하게 1등을 뽑아내고, 나머지 원소에서 1등을 계속 뽑아내면서 정렬한다.
< 버블 정렬과 다른 점 >
버블 정렬: 남은 원소에서 1등을 다시 비교를 통해서 찾는다.
힙 정렬: 힙을 이용하면, 1등을 뽑아낸 뒤 나머지 원소에서 1등을 뽑을 때, 다시 비교할 필요 없이 2등이 자동으로 1등이 된다.
=> 힙 생성 -> 루트 원소 제거 -> 힙을 유지
힙 (Heap)
- 완전 이진 트리이다.
+ 원소가 n개인 힙의 모양은 1개이다. (높이는 logn)
최대 힙: 부모 노드의 키 값이 자식 노드보다 크거나 같은 완전 이진 트리
최소 힙: 부모 노드의 키 값이 자식 노드보다 작거나 같은 완전 이진 트리
=> 트리를 포인터없이 배열로 표현 할 수 있다. (인덱스로 접근)
- i 노드의 부모: i // 2
- i 노드의 왼쪽 자식: 2 × i
- i 노드의 오른쪽 자식: 2 × i + 1
< 힙에서 루트 원소 제거 과정 >
1. 가장 마지막 원소(사라져야 할 위치의 원소)가 루트(빈 자리)로 이동한다.
+ 1개가 제거된 힙의 모양은 이미 결정되어있기 때문에 사라져야 할 원소가 정해진다.
2. 가장 마지막 원소와 원래 노드의 두 자식의 값을 비교하여 가장 큰 (작은) 원소가 올라간다. (위치 변경)
3. 빈 자리가 다시 생겨서 해당 크기의 힙의 모양이 아니라면, 2를 반복한다.
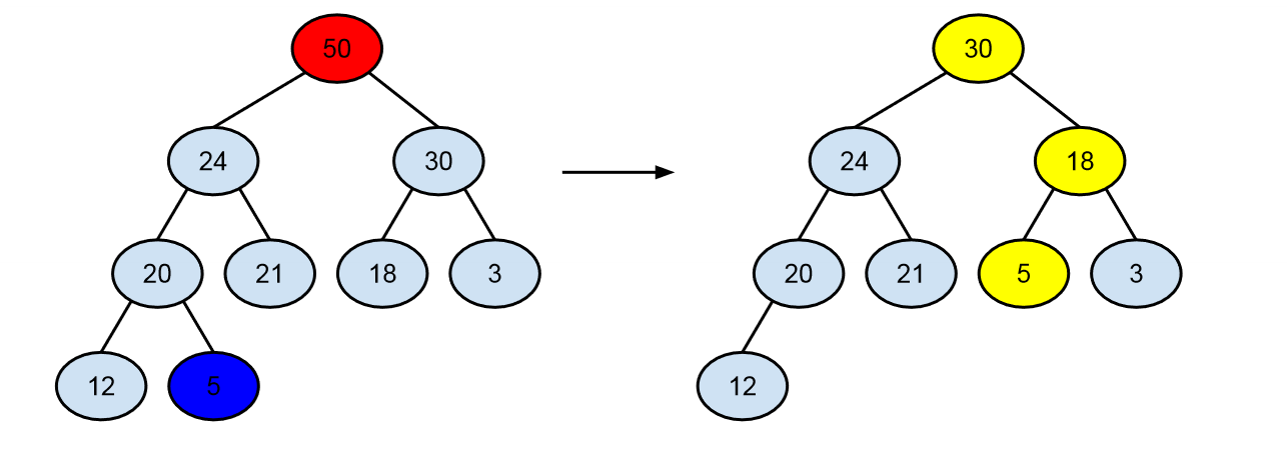
=> 힙이 이미 존재할 때 힙 정렬의 시간 복잡도: log1 + log 2 + ... + logn ≤ logn + logn + ... + logn = Θ(nlogn)
< 힙 생성 과정 1 >
1. 새로운 원소가 들어올 때마다 부모와 비교하여 큰(작은) 값이 올라간다.
+ 새로운 원소가 들어갈 위치는 정해져 있다.
2. 1을 새로운 원소가 루트가 되거나, 부모가 더 큰(작은) 값이 될 때까지 반복한다.
< 힙 생성 과정 2 >
1. 배열을 한 번에 입력 받아서 완전 이진트리를 생성한다.
2. 맨 밑의 원소가 1개인 힙부터, 3개인 힙, 7인 힙, ... , 2^n-1개인 힙을 수정해나간다. (힙 병합)
+ 원소가 1개는 힙이다.
3. 힙을 병합할 때마다 루트 노드부터 리프 노드까지 비교하여 위치를 변경한다.
+ 병합할 힙의 루트 노드부터 자식 노드들과 비교하여 값이 작다면(크다면) 위치를 변경한다.
=> T(n) = 2T(n/2) + logn = Θ(n)
2T(n/2): 왼쪽 트리와 오른쪽 트리를 힙 생성
logn: 두 트리를 병합 (루트부터 노드까지 거리)
즉, 힙 생성 과정 2가 더 빠르다!
'Study > Algorithm Study' 카테고리의 다른 글
| [Algorithm] 정렬: 계수 정렬, 선택 문제 (1) | 2023.10.05 |
|---|---|
| [Algorithm] 정렬: 버킷 정렬, 기수 정렬 (0) | 2023.09.24 |
| [Algorithm] 정렬: 병합 정렬, 퀵 정렬 (1) | 2023.09.17 |
| [Algorithm] 정렬: 버블 정렬, 삽입 정렬 (2) | 2023.09.17 |
| [Algorithm] 알고리즘 기초 (3) (0) | 2023.09.16 |



