[백준/C++] 1002번: 터렛

문제

https://www.acmicpc.net/problem/1002

1002번: 터렛

---

문제 요약

좌표평면에서 두 점 (x1, y1)과 (x2, y2)이 주어졌을 때,

(x1, y1)에서 r1만큼 떨어지고, (x2, y2)에서 r2만큼 떨어진 점의 수를 출력한다.

---

코드

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

int t;

int main() {
    // 입출력 시간 단축
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    cin >> t;

    for (int i = 0; i < t; i++) {
        int x1, y1, r1, x2, y2, r2;

        cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;

        // 두 점 사이의 거리
        double dist = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));

        // 두 원이 일치하는 경우
        if (dist == 0 && r1 == r2)
            cout << -1 << "\n";

        // 두 원이 떨어져 있는 경우
        else if (r1 + r2 < dist || abs(r1 - r2) > dist)
            cout << 0 << "\n";

        // 두 원이 외접하는 경우와 내접하는 경우
        else if (dist == r1 + r2 || dist == abs(r1 - r2))
            cout << 1 << "\n";

        // 두 원이 서로 다른 두 점에서 만나는 경우
        else if (abs(r1 - r2) < dist && dist < r1 + r2)
            cout << 2 << "\n";

        // 하나의 원이 다른 원의 내부에 존재하는 경우
        else
            cout << 0 << "\n";
    }

    return 0;
}

---

코드 설명

좌표평면에서 두 원의 위치관계는 다음과 같다.

 

 

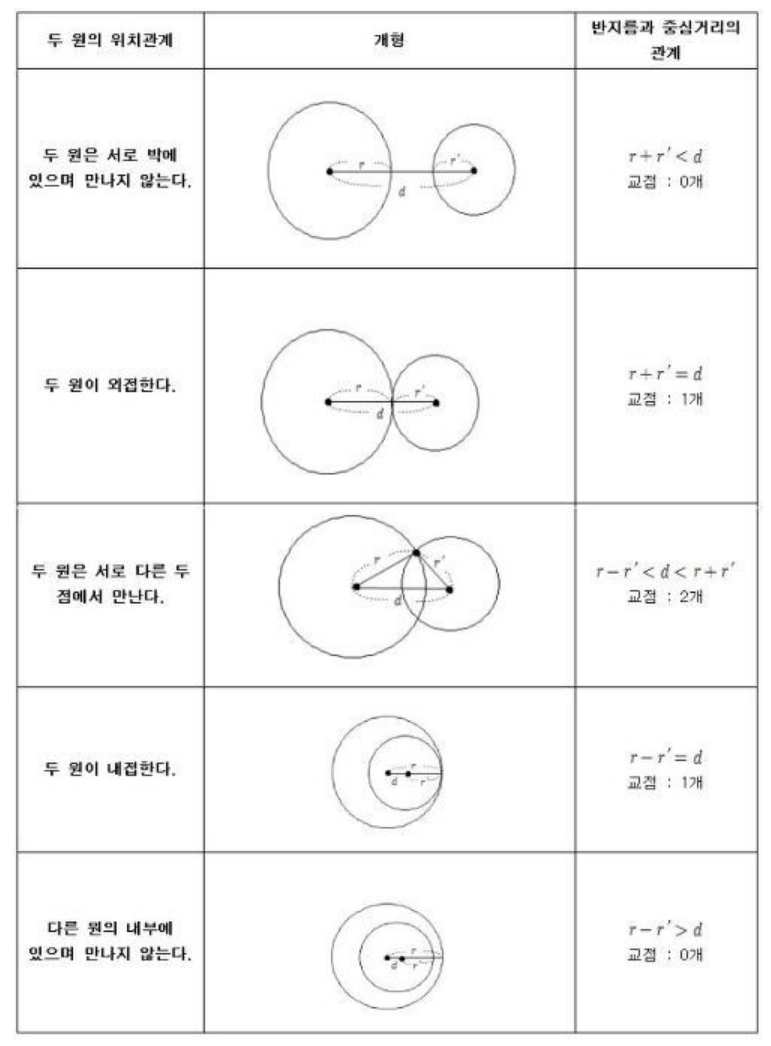
추가적으로, 두 원의 중심과 반지름이 모두 일치하면, 무수히 많은 교점이 발생하므로, -1을 출력한다.