문제
Prefix Sum 배열을 이용하면 누적합을 O(n) 시간에 구할 수 있다.
=> O(logn)에 누적합을 구할 수 있는 방법은 없을까 ?
용어 정의
A[i] : 배열 A의 i번째 요소
L[i] : i를 2진수로 나타냈을 때 마지막 1에 해당하는 값
ex) 12 = 1100 => L[12] = 4
Tree[i] : A[i]부터 앞으로 L[i] 개의 값의 합 (이전 수)

L[i]를 구하는 방법
L[i] = i & -i
-i = ~i + 1
i = 1001101011101011000000000000
~i = 0110010100010100111111111111
-i = 0110010100010101000000000000
i & -i = 000000000000000100000000000
PrefixSum[i]를 구하는 방법
< 예시 >
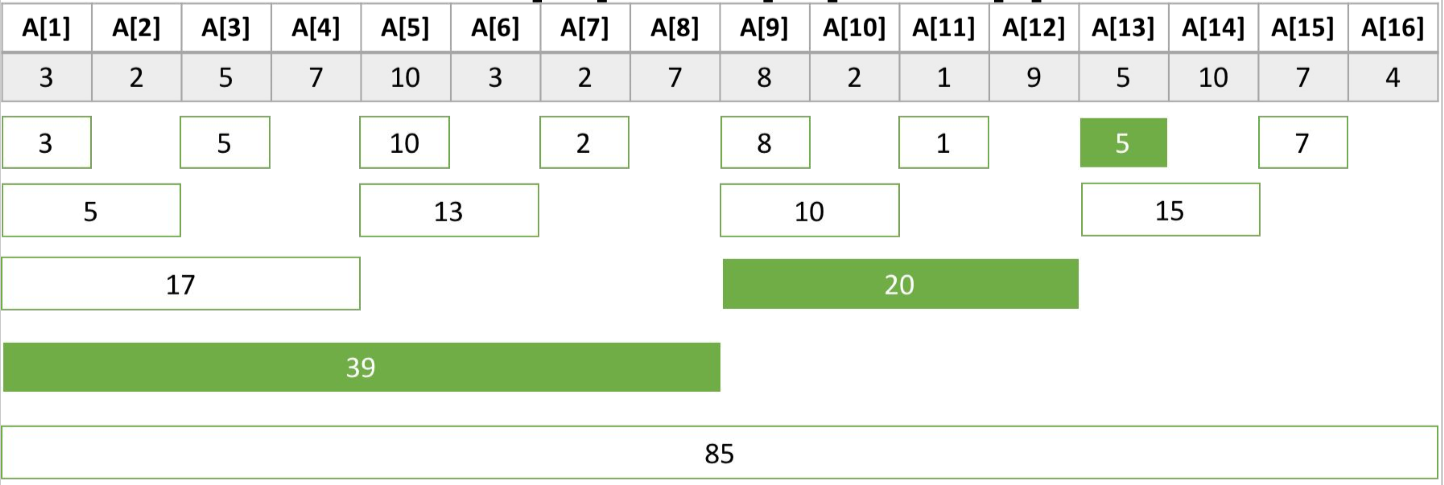
prefix[13]
= Tree[13] + prefix[12]
= Tree[13] + Tree[12] + prefix[8]
= Tree[13] + Tree[12] + Tree[8]
< 검증 >
13 = 8 + 4 + 0 + 1 = 1101 (2)
=> 13번째까지 누적합은 (8 + 4 + 1)번째요소까지 누적합
=> Tree[13] + Tree[12] + Tree[8]
< 코드 >
int sum(int i) {
int ans = 0;
while (i > 0) {
ans += tree[i];
i -= (i & -i);
}
return ans;
}
Update(i, x)
A[i]값이 x로 변경되었을 경우 트리를 갱신해주어야 한다.
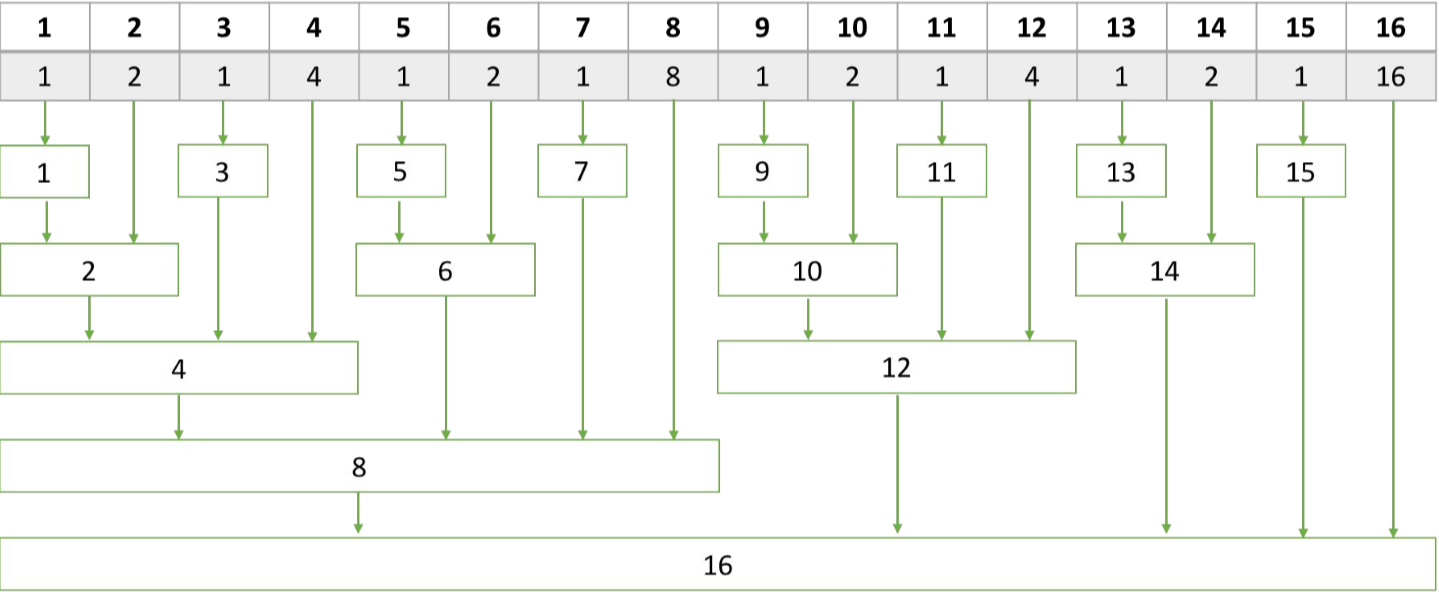
위 사진에서 13번째 값을 갱신되었다면, Tree[13], Tree[14], Tree[16]을 모두 갱신해주어야 한다.
그렇다면, 갱신해야하는 값을 어떻게 알 수 있을까?
< 코드 >
// A[i] 값이 num만큼 증가했을 경우 (A의 길이: n)
void update(int i, int num) {
while (i <= n) {
tree[i] += num;
i += (i & -i);
}
}BIT를 생성하는 방법
먼저, Tree의 모든 값들이 0으로 초기화되어 있다고 가정한다.
A[i] = x가 될 때마다 Update (i. x)를 호출한다.
(최대 logn번 호출될 수 있다.)
생성하는데 O(nlogn), 질의를 처리하는데 O(logn)이 소요된다.
즉, 누적합을 구할 때는 i & -i씩 감소하며 접근해서 값을 더하고,
트리를 갱신할 때는 i & -i씩 증가하며 접근해서 값을 갱신한다.
'Study > Algorithm Study' 카테고리의 다른 글
| [Algorithm] Segment Tree (1) | 2024.06.15 |
|---|---|
| [Algorithm] 해시 테이블 (1) | 2023.11.12 |
| [Algorithm] 탐색 트리 (0) | 2023.11.03 |
| [Algorithm] 정렬: 계수 정렬, 선택 문제 (1) | 2023.10.05 |
| [Algorithm] 정렬: 버킷 정렬, 기수 정렬 (0) | 2023.09.24 |



