+ 한국항공대학교 길현영 교수님의 컴퓨터구조론 과목 내용을 정리한 글입니다.
데이터 종류
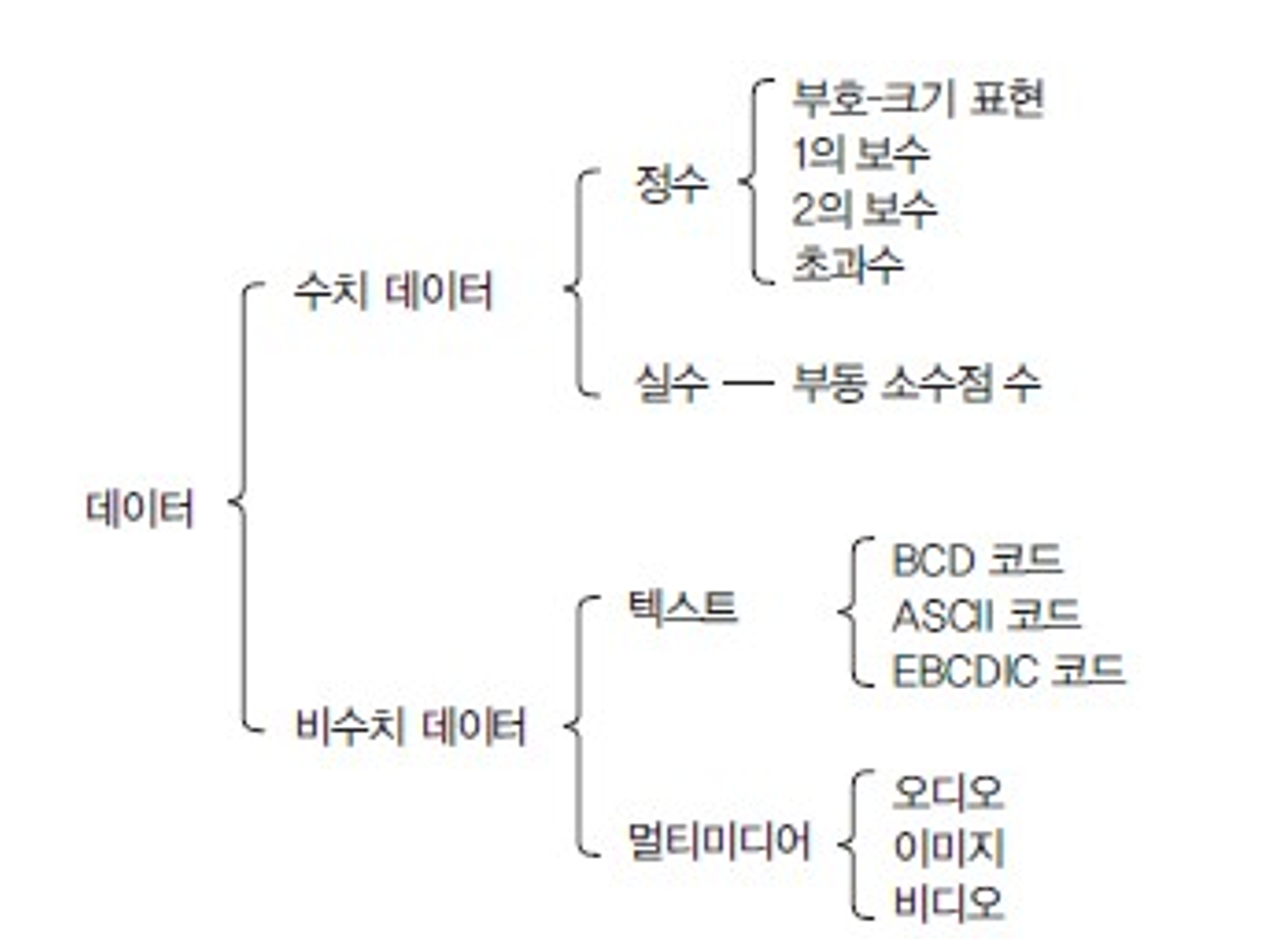
수치 데이터
=> 컴퓨터 내/외부에서 사용
비수치 데이터
=> 컴퓨터 외부에서 사용
데이터 형식
컴퓨터가 지원하는 데이터의 표현 방식이다. (약속)
= 컴퓨터가 제공하는 명령어 집합으로 연산할 수 있는 정보의 표현
(피연산자 뿐 아니라 opcode 역시 포함된다.)
ex)
atomic: 정수(Integer), 불리언(Boolean), 문자(Character), 실수(부동 소수점 수 형태)
complex type: 문자열(String), 배열(Array), 벡터(Vector), 스택(Stack), 큐(Queue)
그러나 모든 컴퓨터(하드웨어)가 모든 데이터 형식을 지원하지 않는다.
- 모든 데이터 형식을 지원하면 하드웨어의 복잡성과 비용이 증가하기 때문이다.
- 컴퓨터마다 지원하는 데이터 형식의 종류가 다르며, 대부분 아키텍쳐는 적은 수의 데이터 형식을 지원한다.
지원되지 않는 데이터 형식은 소프트웨어로 해결한다.
(수치) 데이터와 진법
진법
- 유한한 심볼로 아주 큰 숫자들까지 표현하는 방법
- 10진법: 0~9까지의 10개의 심볼로 무한한 숫자를 표현한다.
ex) 432
= (4 × 10^2) + (3 × 10 ^1) + (2 × 10^0)
다양한 진법들이 존재한다.
컴퓨터는 기본적으로 2진법을 사용한다.
- 메모리, 저장 장치, 네트워크 통신 등 모든 디지털 시스템에서는 2진수로 데이터를 저장하고 처리한다.
- 전기 신호가 통할 때 => 1, 그렇지 않을 때 => 0
2진수
- 0또는 1로 (큰)숫자를 표현하고 비트(binary digit = bit)라고 한다.
=> 대부분의 경우는 최소 단위로 1Byte (= 8bit)를 사용한다.
- 1 Byte는 2진수로 최소 0 ~ 최대 11111111의 값을 표현할 수 있다. (0 ~ 255)
- 즉, 256개의 값들을 표현할 수 있다.
- 더 큰 수를 저장하기 위해서는 2개 이상의 바이트가 필요하다.
=> 디지털 데이터는 2진수를 사용하지만, 모든 데이터를 비트로 나타내면 데이터를 출력, 처리할 때 비효율적이다.
8진수
- 0 ~ 7, 8개의 심볼로 숫자를 표현한다.
- 소수점을 기준으로 왼쪽/오른쪽으로 2진수를 3개씩 묶어서 사용한다.
ex) 000001101 (2)
= 015 (8)
= (1 × 8^1) + (5 × 8^0) = 13
16진수
- 0 ~ 9 + A(10) ~ F(15), 16개의 심볼로 숫자를 표현한다.
- 소수점을 기준으로 왼쪽/오른쪽으로 2진수를 4개씩 묶어서 사용한다.
10진수 -> 2진수 변환
정수 부분과 소수 부분을 각각 2진수로 변환하고, 가운데 소수점을 찍는다.
- 정수 부분: 나누는 부분(몫)이 0이 될 때까지 2로 나누고 나머지를 역순으로 나열한다.
- 소수 부분: 곱할 부분(소수)이 1이 될때까지 2로 곱하고 정수를 나열한다.
ex)13.6875 = 13 (정수 부분) + 0.6875 (소수 부분)
1) 13 ÷ 2 = 6 ... 1
2) 6 ÷ 2 = 3 ... 0
3) 3 ÷ 2 = 1 ... 1
4) 1 ÷ 2 = 0 ... 1
=> 11(정수 부분)의 2진수 표현: 1101
5) 0.6875 × 2 = 1.375 (정수: 1, 소수: 0.375)
6) 0.375 × 2 = 0.75 (정수: 0, 소수: 0.75)
7) 0.75 × 2 = 1.5 (정수: 1, 소수 0.5)
8) 0.5 × 2 = 1 (정수: 1, 소수: 0)
=> 0.6875(소수 부분)의 2진수 표현: 1011
=> 1101.1011
2진수 -> 10진수 변환
2진수의 각 자리 숫자를 2의 지수 승에 맞추어서 더한다.
ex) 1101.1011
= (1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0) + (1 × 2^-1) + (0 × 2^-2) + (1 × 2^-3) + (1 × 2^-4)
= 8 + 4 + 0 + 1 + 0.5 + 0 + 0.125 + 0.0625
=> 13.6875
2진수 -> 8진수 변환
정수 부분은 소수점을 기준으로 왼쪽 방향으로 3자리, 소수 부분은 소수점을 기준으로 오른쪽 방향으로 3자리씩 묶어서 변환한다.
ex) 1101.1011
= 001 / 101 . 101 / 100
=> 15.54
2진수 -> 16진수 변환
- 정수 부분은 소수점을 기준으로 왼쪽 방향으로 4자리, 소수 부분은 소수점을 기준으로 오른쪽 방향으로 4자리씩 묶어서 변환한다.
ex) 1101.1011
= 1101 . 1011
=> D.B
8진수 -> 2진수 변환
8진수 1자리를 2진수 3비트로 풀어서 변환한다.
ex) 15.54
= 001 / 101 . 101 / 100
=> 1101.1011
16진수 -> 2진수
- 16진수 1자리를 2진수 4비트로 풀어서 변환한다.
ex) D.B
= 1101 . 1011
=> 1101.1011
데이터의 물리적 단위
실제 물리적 장치에서 사용되는 단위로, bit가 최소 표현 단위이다.
저장 장치의 용량이 증가하면서, byte가 주로 사용된다.

+ 대략적으로 1000배씩 증가한다. (1024 = 2^10)
참고: Niblle = 4bit
보수
'상호 보완하는 수'라는 의미로, 어떤 수를 보완해주는 다른 임의의 수이다.
r진법에서는 (r-1)의 보수와 r의 보수가 존재한다.
- A에 대한 (r-1)의 보수 B: 두 개의 숫자 (A, B)들을 더한 결과의 각 자리가 (r-1) 되는 B
ex) 237에 대한 9의 보수: 237 + B = 999, B = 762
- A에 대한 r의 보수 B: 두 개의 숫자 (A, B)들을 더한 결과의 각 자리마다 올림이 발생하고 각 자리는 0이 되는 B
ex) 237에 대한 10의 보수: 237 + B = 1000, x = 762
보수를 이용하여 음수를 표현할 수 있다.
a - b = a + (-b) 이용
ex)
48의 10의 보수 = 100 - 48 = 52
48의 9의 보수 = 99 - 48 = 51
90 - 48 = 42
1. 9의 보수 이용: 90 + 52 = 142 => 42 (올림 자리를 버리면)
2. 10의 보수 이용: 90 + 51 = 141 => 42 (올림 자리를 더하고 버리면)
정수 표현
고정 소수점 (fixed point) 형태로 사용한다.
- 정수 데이터의 표현과 연산에 사용하는 방식이다.
- 소수점은 맨 오른쪽에 있는 것으로 가정한다.
ex) 2 = 2.
1. 무부호 정수 표현 방식(양수)
- 부호 bit가 없는 형태이다.
- n bit의 경우 2^n개의 숫자 표현이 가능하다. (표현 가능 수: 0 ~ 2^n - 1)
- 주소 관련 정보 표현을 위해 사용하나, 음수 표현이 어려워 일부 아키텍쳐만 지원한다.
2. 부호 - 크기 표현 방식
- 최상위 1비트 (MSB, Most Significant Bit): 부호 비트 (양수: 0, 음수: 1)
- 나머지: 크기 필드
- 표현 가능 범위: -(2^n-1 - 1) ~ -0, +0 ~ 2^n-1 - 1
- 자릿수 확장 시, 부호 비트를 제외한 나머지 크기 부분만 0을 넣어서 확장한다.
ex) 4bit 표현 1101 -> 32bit 표현: 1000 0000 0000 0000 0000 0000 0000 0101
- 장점: 부호 비트만 바꾸면 양수를 음수로, 음수를 양수로 변환할 수 있다.
- 단점: 2개의 0, 즉 +0과 -0이 존재한다.
연산 수행 시 두 숫자의 부호에 따라 연산 방법이 다르므로 부호를 별도로 점검해야한다.
덧셈 연산을 위해 덧셈, 뺄셈 장치가 모두 필요하다.
ex) 동일한 부호일 때 덧셈: 크기 부분을 더하고, 부호 비트를 추가한다.
ex) 다른 부호일 때 덧셈: 크기 부분의 차이(뺄셈)를 구하고, 크기(절댓값)가 큰 수의 부호를 적용한다.
=> 즉, 덧셈 연산을 하는데 덧셈 장치와 뺄셈 장치가 모두 필요하다.

3. 1의 보수 표현 방식
- n bit 정수의 경우, 양의 2진수 x의 1의 보수는 (2^n - 1) - x
ex) n = 4, (2^n - 1) = 1111, -2 = +2 (0010)의 1의 보수 = 1111 - 0010 = 1101
=> 0과 1을 상호 반전한 값과 같다. (+2 = 0010, -2 = 1101)
- 표현 가능 범위: -(2^n-1 - 1) ~ -0, +0 ~ 2^n-1 - 1 (부호 - 크기 방식과 표현 방식만 다르다.)
- 자릿수 확장 시, 부호 비트를 제외한 나머지 크기 부분만 부호 비트을 넣어서 확장한다.
ex) +5 4bit 표현 0101 -> 32bit 표현: 0000 0000 0000 0000 0000 0000 0000 0101
ex) -5 4bit 표현 1010 -> 32bit 표현: 1111 1111 1111 1111 1111 1111 1111 1010
- 장점: 음수와 양수의 변환이 용이하다.
- 단점: 2개의 0, 즉 +0(0000)과 -0(1111)이 존재한다
+ 부호와 상관없이 연산 방법이 같으나, 순환 자리 올림이 발생한다.
MSB에서 올림수가 발생하면 연산결과에 올림수를 더해야 한다. (두 개의 0이 있기 때문에 발생한다.)
ex)-0에서 1을 더하면 +0이다.

4. 2의 보수 표현 방식
- n bit 정수의 경우, 양의 2진수 x의 2의 보수는 2^n - x
ex) n = 4, 2^n = 10000, -2 = +2 (0010)의 2의 보수 = 10000 - 0010 = 1110
=> 1의 보수에 1을 더한 값과 같다. (+2 = 0010, +2의 1의 보수 = 1101, -2 = 1110)
- 표현 가능 범위: -2^n-1 ~ 0, ~ 2^n-1 - 1 (다른 방식보다 음수에서 1개 더 표현할 수 있다.)
ex) -8 = 1000
- 자릿수 확장 시, 부호 비트를 제외한 나머지 크기 부분만 부호 비트을 넣어서 확장한다.
ex) +5 4bit 표현 0101 -> 32bit 표현: 0000 0000 0000 0000 0000 0000 0000 0101
ex) -5 4bit 표현 1010 -> 32bit 표현: 1111 1111 1111 1111 1111 1111 1111 1010
- 장점: 1개의 0이 존재한다.
- 단점:음수와 양수의 변환이 1의 보수에 1을 더하는 추가 과정이 필요하다.
+ 전환은 번거롭지만 덧셈 장치만으로 연산이 가능하고, 한 개의 0으로 순환자리올림이 없다.
=> 2의 보수 표현 방식을 많이 사용한다.
실수 표현
부동 소수점 (floating point) 형태로 사용한다.
- 정수 및 연속한 두 정수 사이의 모든 수를 표현한다.
과학적 표기법 및 부동 소수점 형태로 표현한다.

s: 부호
M: 가수 (유효 숫자)
R: 기수
E: 지수

부동 소수점은 하나의 실수가 무한한 방법으로 표현이 가능하다. (비정규화수)
ex) 0.00613 × 10^1
= 0.0613 × 10^0
= 0.613 × 10^-1
= 6.13 × 10^-2
= 61.3 × 10^-3
=> 컴퓨터는 표준화된 표현방식이 필요하다.
정규화 수 (normalized number)
- 소수점 왼쪽에 있는 수를 0이 아닌 한 자리 수로 표현한다.
2진법을 사용하는 정규화된 실수
- 편의상 가수만 2진수 나머지 지수와 기수는 10진수로 표현한다.
ex) 1.001 × 2^5
소수점 왼쪽 정수값이 0이 되거나 1bit를 넘는다면 Shift 연산을 통해 정규화해야한다.
ex) 0.0101 -> 1.01 × 10^-2, 11.01 -> 1.101 × 10^1

비수치 데이터
BCD 코드 (Binary Coded Decimal)
- 2진화 10진 코드라고도 불린다.
- 숫자, 알파벳, 특수 기호를 나타내기 위해 6 bit로 구성된 코드이다. (2^6개 표현 가능)
- 실제로는 오류 검출용 패리티를 위한 1 bit를 포한하여 7 bit로 구성되어 있다.
미국정보교환표준부호 (ASCII, American Standard Code for Info. Interchange)
- 미국국립표준연구소가 제장한, 알파벳을 사용하는 대표적인 문자 코드이다.
- 데스크톱 컴퓨터와 같은 소형 컴퓨터를 중심으로 보급되어 현재 국제적으로 널리 사용된다.
- 8 bit = 1 bit(패리티 비트) + 3 bit(영역 비트) + 4 bit(숫자 필드)
유니코드
- 다국적 알파벳을 대부분 포함하기 위해 하나의 문자를 16 bit 체계로 구성한 코드이다.
- 현재 대부분의 시스템이나 애플리케이션에서 점진적으로 ASCII코드를 대신하는 추세이다.
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] 데이터 연산 (picoMIPS) (1) | 2023.10.22 |
|---|---|
| [Computer Architecture] 디지털 논리 회로 (2) | 2023.10.22 |
| [Computer Architecture] picoMIPS 명령어 집합 구조 (2) | 2023.10.15 |
| [Computer Architecture] CISC & RISC (49) | 2023.10.08 |
| [Computer Architecture] 주소 지정 방식 (0) | 2023.10.07 |



