+ 한국항공대학교 길현영 교수님의 컴퓨터구조론 과목 내용을 정리한 글입니다.
CPU의 연산장치 (ALU, Arithmetic & Logic Unit)
+,- 등 산술 연산, AND, OR 등 논리 연산, Shifter, 보수기 등이 포함된다.
- << 연산: × 2^n
- >> 연산: ÷ 2^n
ex) add $5 $3 $ 4: 레지스터 3에 저장된 데이터와 레지스터 4에 저장된 데이터를 더하고 레지스터 5에 저장
=> 0000 011 100 101 010 (순서 기억)
1. OpCode와 fn을 통해 명령어를 해독한다.
- ALU에 + 제어신호를 전달한다.
=> R-형식 명령어 이므로 3bit(source), 3bit(target), 3bit(destination) 레지스터의 주소임을 인식한다.
2. source, target 레지스터 주소에 해당하는 데이터를 가져와서 ALU에서 더하기 연산을 진행한다.
- 레지스터 주소는 3bit, 레지스터 데이터는 16bit이다.
3. 연산을 진행한 데이터를 destination 레지스터 주소에 저장한다.
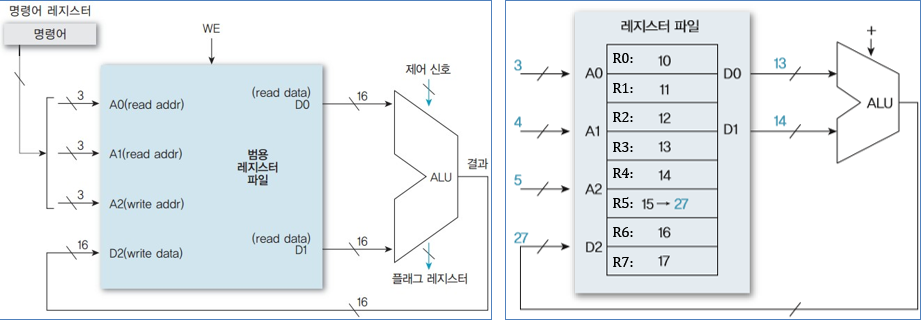
ALU 내 산술장치와 논리장치의 통합
16bit의 산술장치와 논리장치를 멀티플렉서를 이용하여 연결한다.
2개의 16bit 입력 데이터가 산술장치와 논리장치에 입력된다.
- 입/출력 올림수는 산술장치에만 각각 입력되고 출력된다.
3bit 제어 신호에 따라 어떤 장치를 선택할지 결정한다.
- 2bit는 산술장치와 논리장치에 입력되어 각 장치의 연산 종류를 선택한다.
- 1bit는 멀티플렉서에 적용되어 산술장치와 논리장치 출력 중 하나를 선택하여 출력한다.

Flag register
CPU내 연산 과정 중에 발생한 상태 데이터들을 저장한다.
- 하나의 정답 값 외에 발생하는 부수적 정보 데이터: 올림수(C), 오버플로우(V), 부호(S), 0값(Z)
ex) 11 + 11 = 110 (올림수 발생), 16bit + 16bit = 17bit (오버 플로우 발생), 11 - 11 = 00 (0값)
프로그램을 제어할 때 많이 사용된다.
ex) beq 분기 명령어를 수행 시 Z값을 체크한다. (연산 결과값이 0이면 Z = 1)
정수의 뎃셈
10진수 덧셈과 유사하다.
- 오른쪽(낮은 자리) -> 왼쪽(높은 자리)으로 한 자리씩 더하고, 올림수 발생 시 함께 더한다.
두 수의 부호가 다를 때: 절댓값이 큰 수의 부호를 따라간다. (자리올림수 무시)
두 수의 부호가 같을 때: 자리올림수(잉여 비트)를 무시한 결과는 오버플로우가 발생가능하다.
+ 오버플로우: 두 정수의 연산 결과가 주어진 비트로 표현할 수 없는 경우
ex) 운이 좋은 경우
1. (+3) + (+4) = +7
=> 0011 + 0100 = 0111
2. (-3) + (+3) = 0
=> 1101 + 0011 = (1)0000 (Overflow가 아닌 Carry)
3. (-6) + (+2) = -4
=> 1010 + 0010 = 1100
4. (-4) + (-1) = -5
=> 1100 + 1111 = (1)1011
ex) 오버플로우 발생 예시(-3) + (-6) = -9=> 1101 + 1010 = (1)0111즉, -9가 아닌 7이 답이 된다.
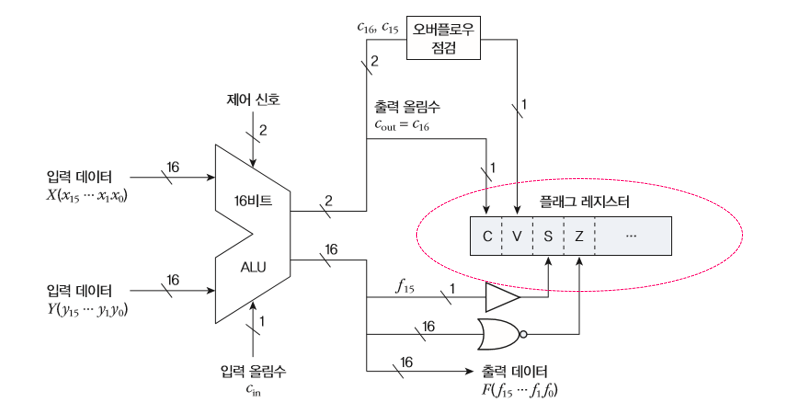
< 오버 플로우 점검 방법 >
MSB(가장 큰 자릿수)에 대한 입력 올림수(Carry In)와 출력 올림수(Carry Out)가 서로 다를 때 발생한다.
- XOR 게이트를 이용하여 구현 가능하다.

=> 즉 점검하여 오버 플로우라면 표현을 못하는 상황이고, 아니라면 비트를 벗어나는 잉여 비트를 지운다.
< 두 수의 비트 수가 다를 때 >
부호 확장을 통해 동일한 비트 수로 변환해야한다.
- 비트 수가 작은 수를 큰 수의 비트 수로 변환해야한다.

4 bit 정수의 덧셈 뺄셈 장치
4개의 전가산기(FA, Full Adder)를 직렬로 연결한다.
뺄셈의 경우, 빼야할 숫자를 2의 보수로 변환하여 덧셈을 수행한다.
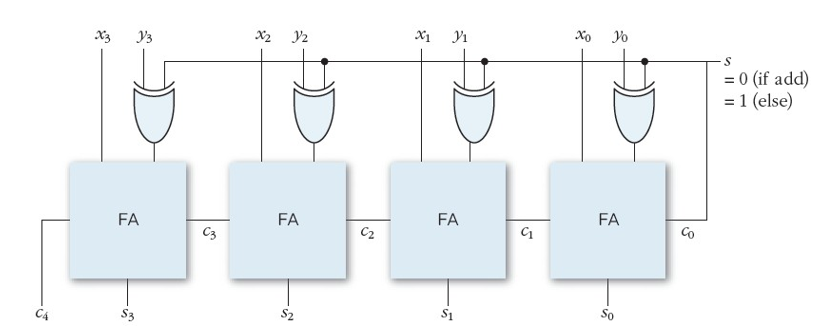
s는 제어신호로 뺄셈일 경우, 2의 보수 처리를 위해 +1을 갖는다.
- C는 자리 올림수이다. 그 중 C0는 2의 보수 처리를 위해 1의 보수에서 +1 역할을 한다.
무부호 정수의 곱셈
종이 - 연필 방식

=> N bit 수 2개를 곱셈했을 때, 결과는 최대 2N bit이다.
즉, 2N bit 덧셈연산장치가 필요하다.
부분곱의 개수는 승수를 구성하는 비트 수와 동일하다.
-> 일반적으로 컴퓨터의 연산 장치는 2개의 입력을 받아 1개의 출력을 생성하는 회로로 설계한다.
-> 부분곱 3개 이상을 한 번에 입력하는 계산을 원한다면 따로 추가적인 설계가 필요하다.
시프트 - 덧셈 방식 (1)
각 사이클마다 승수(부분곱)를 왼쪽으로 1-Shift하고, 누적 부분곱에 부분곱을 더한다.
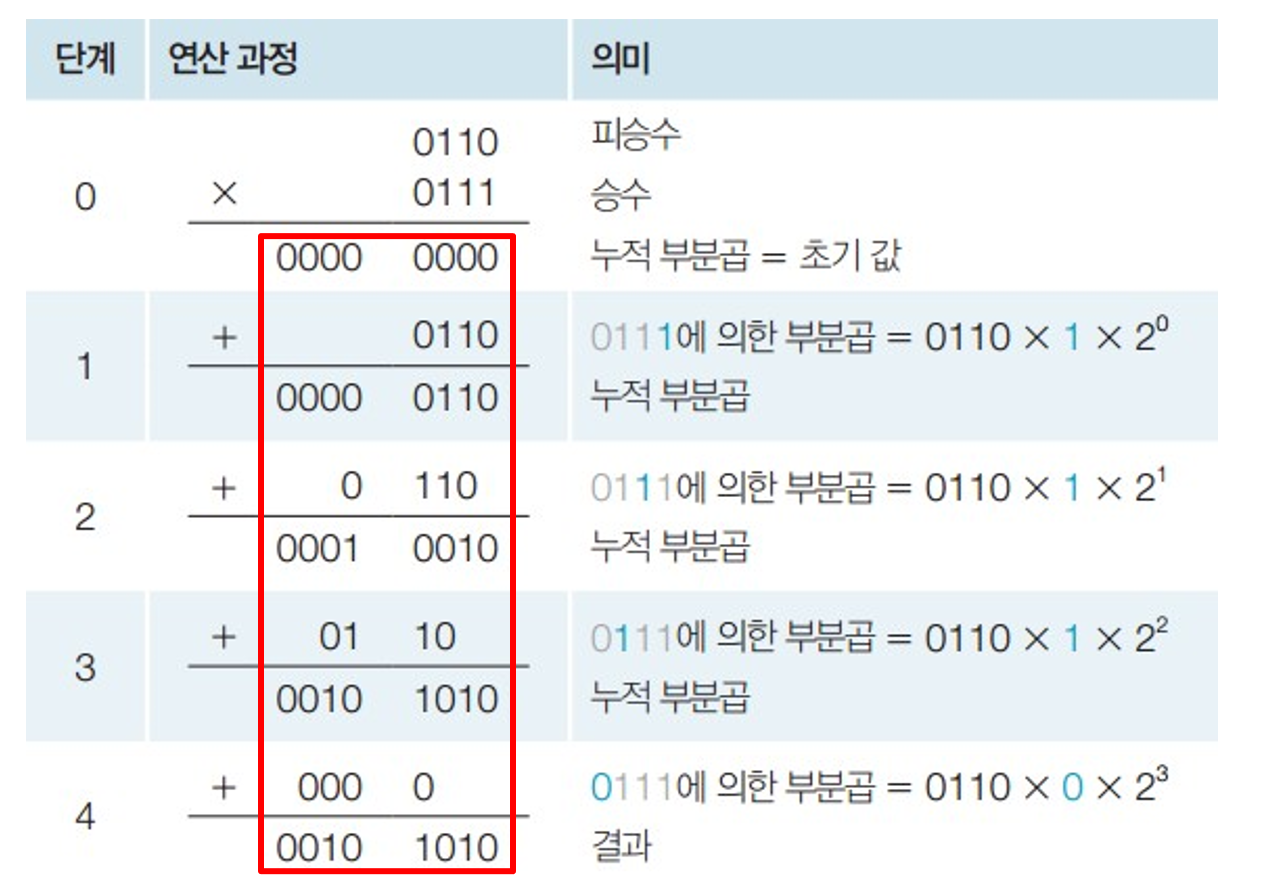
=> 부분곱 계산을 위해 2N bit 덧셈 연산이 필요하다. (HW 낭비)
시프트 - 덧셈 방식 (2)
N bit 덧셈장치로 N bit 곱셈장치를 구현한다.
- 상위 N bit만 덧셈을 수행한다.
미리 4 bit 왼쪽 Shift한 승수를 사이클마다 누적 부분곱에 더한 후, 누적 부분곱을 1 bit씩 오른쪽 시프트한다.

=> 승수에 1이 많을수록 덧셈이 증가한다.
Booth 알고리즘
< 10진법 >
A × 9999
= A × (9 + 90 + 900 + 9000)
=> 곱셈 4번과 덧셈 3번이 필요하다.
= A × (10000 - 1)
=> 곱셈 2번과 덧셈(뺄셈) 1번만 필요하다.
< 2진법 >
A × 01111110
= A × (01000000 + 00100000 + 00010000 + 00001000 + 00000100 + 00000010)
=> 곱셈 6번과 덧셈 5번이 필요하다.
= A × (10000000 - 00000010)
=> 곱셈 2번과 덧셈(뺄셈) 1번만 필요하다.
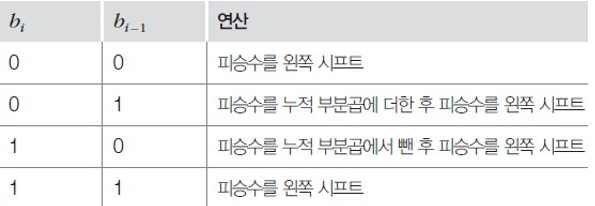

+ booth 알고리즘은 음수 × 양수도 가능하다.
무부호 정수의 나눗셈
피제수(D, dividend), 제수(V, divisor), 몫(Q, quotient), 나머지(R, remainder)
=> D ÷ V = Q ... R
=> D = Q × V + R
Q와 V가 n비트라면 D의 비트 수는 2 × n 비트도 가능하다.
- n bit 나눗셈 시, 피제수의 bit를 2n bit로 확장하기도 한다.
종이 - 연필 방식
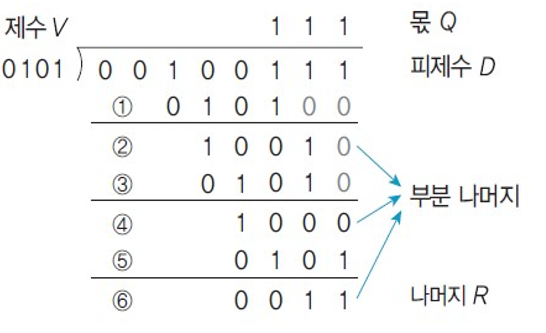
컴퓨터는 몫이 시작하는 자리를 찾을수 있는가?
=> 피제수와 제수의 뺄셈을 통해 비교하여 크기를 비교해야한다.
복원 알고리즘

뺄셈한 결과인 부분 나머지가 음수이면, 다시 제수를 더한 다음, 더 큰 수에서 빼기 위해 피제수를 1비트씩 왼쪽으로 시프트하면서 제수를 빼는 과정을 반복하므로써 몫과 나머지를 구한다.
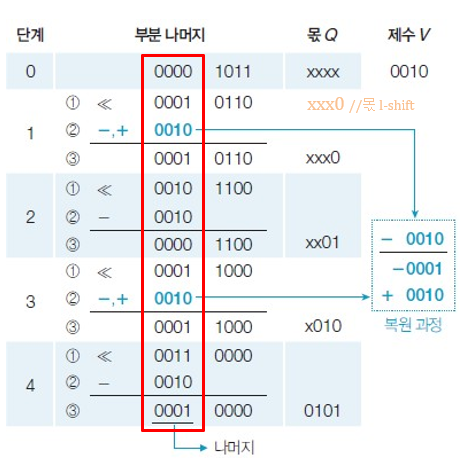
< 계산 과정 >
0. 초기의 부분 나머지는 피제수를 n비트에서 2n비트로 확장한다.
1. 부분 나머지를 1 bit 왼쪽으로 Shift한다. 부분 나머지의 왼쪽 n bit에서 제수를 뺀다.
- 뺄셈 결과가 음수이면, 몫의 LSB에 0을 추가하고 제수를 다시 덧셈하여 부분 나머지를 복원한다.
- 뺄셈 결과가 음수가 아니라면, 몫의 LSB에 1을 추가한다.
2. 1을 n번 반복한다.
=> 뺄셈 연산 후 복원 여부에 따라 덧셈을 수행하므로 오랜 시간이 소요된다.
비복원 알고리즘

(1 × 2^n) - (1 × 2^n-1) = (1 × 2^n-1) 임을 이용한다.
< 계산 과정 >
1. 제수를 오른쪽 Shift한다. (÷ 2)
2. 부분 나머지가 음수면 제수를 더하고 음수가 아니면 제수를 뺀다.
3. 부분 나머지가 음수이면 대응하는 몫의 LSB에 0을, 아니면 1을 추가한다.
+ 제수를 오른쪽으로 Shift하는 것과 피제수 또는 부분 나머지를 왼쪽으로 Shift하는 것은 같은 의미이다.
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] 파이프라이닝 (1) | 2023.11.11 |
|---|---|
| [Computer Architecture] 데이터 경로 (0) | 2023.11.05 |
| [Computer Architecture] 디지털 논리 회로 (2) | 2023.10.22 |
| [Computer Architecture] 데이터 표현 (1) | 2023.10.15 |
| [Computer Architecture] picoMIPS 명령어 집합 구조 (2) | 2023.10.15 |



